Start here for terminology.
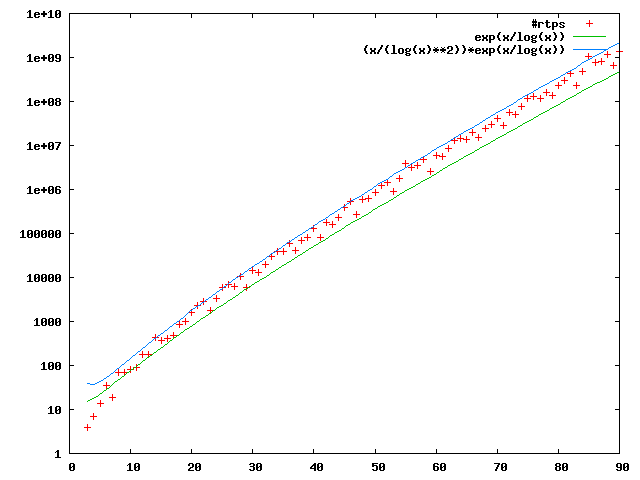
Here is a plot of the number of rtp's for each base, based upon the table below, and two functions which seem to bound above and below. Also in the table is the number of rtp leaders (leaf nodes, numbers with no children), the ratio of leaders, and the number of digits of the largest rtp in that base. The ratio of rtp's which are leaders can be seen to be roughly constant, independent of the base (~1/2.74). If you follow the links for each base, a complete record of how many rtps and leaders were found with each number of digits fan be found.

| base | tally | leaders | leader ratio | digits | most common length reality / predicted | |
|---|---|---|---|---|---|---|
| 3 | 4 | 1 | 0.25000 | 4 | 1 of length 1 | 2.73 |
| 4 | 7 | 2 | 0.28571 | 4 | 2 of length 1 | 2.89 |
| 5 | 14 | 4 | 0.28571 | 5 | 4 of length 2 | 3.11 |
| 6 | 36 | 11 | 0.30556 | 7 | 9 of length 5 | 3.35 |
| 7 | 19 | 7 | 0.36842 | 5 | 6 of length 3 | 3.60 |
| 8 | 68 | 20 | 0.29412 | 8 | 16 of length 4 | 3.85 |
| 9 | 68 | 23 | 0.33824 | 10 | 14 of length 4 | 4.10 |
| 10 | 83 | 27 | 0.32530 | 8 | 16 of length 4 | 4.34 |
| 11 | 89 | 28 | 0.31461 | 10 | 20 of length 4 | 4.59 |
| 12 | 179 | 61 | 0.34078 | 10 | 34 of length 4 | 4.83 |
| 13 | 176 | 61 | 0.34659 | 10 | 28 of length 4 | 5.07 |
| 14 | 439 | 153 | 0.34852 | 17 | 74 of length 5 | 5.30 |
| 15 | 373 | 130 | 0.34853 | 13 | 74 of length 6 | 5.54 |
| 16 | 414 | 151 | 0.36473 | 14 | 77 of length 6 | 5.77 |
| 17 | 473 | 157 | 0.33192 | 18 | 79 of length 5 | 6.00 |
| 18 | 839 | 301 | 0.35876 | 15 | 129 of length 5 | 6.23 |
| 19 | 1010 | 343 | 0.33960 | 15 | 165 of length 6 | 6.45 |
| 20 | 1577 | 561 | 0.35574 | 17 | 242 of length 7 | 6.68 |
| 21 | 2271 | 806 | 0.35491 | 18 | 343 of length 7 | 6.90 |
| 22 | 2848 | 1046 | 0.36728 | 20 | 426 of length 7 | 7.12 |
| 23 | 1762 | 615 | 0.34904 | 15 | 260 of length 6 | 7.34 |
| 24 | 3376 | 1227 | 0.36345 | 24 | 508 of length 8 | 7.55 |
| 25 | 5913 | 2136 | 0.36124 | 18 | 836 of length 8 | 7.77 |
| 26 | 6795 | 2472 | 0.36380 | 19 | 959 of length 8 | 7.98 |
| 27 | 6352 | 2288 | 0.36020 | 21 | 921 of length 8 | 8.19 |
| 28 | 10319 | 3685 | 0.35711 | 21 | 1420 of length 8 | 8.40 |
| 29 | 5866 | 2110 | 0.35970 | 22 | 833 of length 8 | 8.61 |
| 30 | 14639 | 5241 | 0.35802 | 22 | 1976 of length 9 | 8.82 |
| 31 | 13303 | 4798 | 0.36067 | 22 | 1800 of length 9 | 9.03 |
| 32 | 19439 | 7017 | 0.36098 | 23 | 2594 of length 9 | 9.23 |
| 33 | 29982 | 10630 | 0.35455 | 23 | 3874 of length 9 | 9.44 |
| 34 | 38956 | 14175 | 0.36387 | 25 | 4891 of length 10 | 9.64 |
| 35 | 39323 | 14127 | 0.35926 | 24 | 5164 of length 10 | 9.84 |
| 36 | 58857 | 21267 | 0.36133 | 24 | 7304 of length 10 | 10.05 |
| 37 | 41646 | 15034 | 0.36100 | 26 | 5291 of length 10 | 10.25 |
| 38 | 68371 | 24677 | 0.36093 | 27 | 8479 of length 10 | 10.45 |
| 39 | 80754 | 29289 | 0.36269 | 27 | 9971 of length 10 | 10.65 |
| 40 | 128859 | 46814 | 0.36330 | 29 | 15646 of length 11 | 10.84 |
| 41 | 81453 | 29291 | 0.35961 | 26 | 10084 of length 10 | 11.04 |
| 42 | 175734 | 63872 | 0.36346 | 29 | 20909 of length 11 | 11.24 |
| 43 | 161438 | 58451 | 0.36206 | 30 | 19522 of length 11 | 11.43 |
| 44 | 228543 | 82839 | 0.36247 | 27 | 27028 of length 11 | 11.63 |
| 45 | 396274 | 143678 | 0.36257 | 31 | 45758 of length 12 | 11.82 |
| 46 | 538797 | 196033 | 0.36383 | 31 | 61124 of length 12 | 12.01 |
| 47 | 273372 | 99103 | 0.36252 | 28 | 32102 of length 11 | 12.21 |
| 48 | 600894 | 218108 | 0.36297 | 32 | 68242 of length 12 | 12.40 |
| 49 | 613153 | 222510 | 0.36289 | 32 | 70087 of length 12 | 12.59 |
| 50 | 851776 | 309795 | 0.36370 | 33 | 94870 of length 13 | 12.78 |
| 51 | 1207819 | 438120 | 0.36274 | 35 | 133850 of length 13 | 12.97 |
| 52 | 1409069 | 512532 | 0.36374 | 36 | 155347 of length 13 | 13.16 |
| 53 | 882292 | 320570 | 0.36334 | 31 | 98582 of length 13 | 13.35 |
| 54 | 1822500 | 662353 | 0.36343 | 36 | 197583 of length 13 | 13.54 |
| 55 | 3957757 | 1436791 | 0.36303 | 38 | 418106 of length 14 | 13.72 |
| 56 | 3108736 | 1129323 | 0.36327 | 37 | 331798 of length 14 | 13.91 |
| 57 | 3578161 | 1302148 | 0.36392 | 36 | 379556 of length 14 | 14.10 |
| 58 | 4684372 | 1706586 | 0.36431 | 37 | 487922 of length 14 | 14.28 |
| 59 | 2520986 | 916564 | 0.36357 | 35 | 270139 of length 14 | 14.47 |
| 60 | 5953742 | 2165044 | 0.36364 | 38 | 618382 of length 15 | 14.65 |
| 61 | 5524486 | 2010149 | 0.36386 | 38 | 577934 of length 14 | 14.84 |
| 62 | 8637410 | 3142426 | 0.36382 | 40 | 890724 of length 15 | 15.02 |
| 63 | 13021368 | 4741075 | 0.36410 | 39 | 1328458 of length 15 | 15.21 |
| 64 | 14216545 | 5179962 | 0.36436 | 41 | 1439695 of length 15 | 15.39 |
| 65 | 13966133 | 5080251 | 0.36376 | 41 | 1411924 of length 15 | 15.57 |
| 66 | 19977480 | 7270052 | 0.36391 | 40 | 1999328 of length 16 | 15.75 |
| 67 | 15053583 | 5479016 | 0.36397 | 42 | 1520900 of length 15 | 15.93 |
| 68 | 24798760 | 9042306 | 0.36463 | 40 | 2478999 of length 16 | 16.12 |
| 69 | 29483567 | 10743812 | 0.36440 | 43 | 2929014 of length 16 | 16.30 |
| 70 | 41014886 | 14930609 | 0.36403 | 44 | 3992044 of length 17 | 16.48 |
| 71 | 28523639 | 10387112 | 0.36416 | 42 | 2836554 of length 16 | 16.66 |
| 72 | 57176196 | 20847837 | 0.36462 | 47 | 5551985 of length 17 | 16.84 |
| 73 | 49841056 | 18167670 | 0.36451 | 43 | 4851762 of length 17 | 17.01 |
| 74 | 76776947 | 27995174 | 0.36463 | 43 | 7417688 of length 17 | 17.19 |
| 75 | 118408046 | 43194384 | 0.36479 | 47 | 11258834 of length 17 | 17.37 |
| 76 | 133210381 | 48602531 | 0.36486 | 46 | 12594279 of length 18 | 17.55 |
| 77 | 117085262 | 42715311 | 0.36482 | 46 | 11121039 of length 17 | 17.73 |
| 78 | 159081762 | 58099353 | 0.36522 | 47 | 15012447 of length 18 | 17.90 |
| 79 | 136343482 | 49718679 | 0.36466 | 45 | 12897770 of length 18 | 18.08 |
| 80 | 231196364 | 84386310 | 0.36500 | 46 | 21706360 of length 18 | 18.26 |
| 81 | 306202312 | 111723570 | 0.36487 | 47 | 28350090 of length 18 | 18.43 |
| 82 | 432132618 | 157690495 | 0.36491 | 50 | 39722251 of length 19 | 18.61 |
| 83 | 227653799 | 83052016 | 0.36482 | 46 | 21366470 of length 18 | 18.78 |
| 84 | 472550385 | 172534984 | 0.36511 | 49 | 43380865 of length 19 | 18.96 |
| 85 | 1055904209 | 385019981 | 0.36464 | 53 | 94678873 of length 20 | 19.13 |
| 86 | 751059072 | 274077456 | 0.36492 | 49 | 68147522 of length 19 | 19.31 |
| 87 | 832046877 | 303776061 | 0.36509 | 53 | 75107844 of length 19 | 19.48 |
| 88 | 1179350432 | 430660536 | 0.36517 | 52 | 105599217 of length 20 | 19.65 |
| 89 | 643612177 | 234918723 | 0.36500 | 50 | 58700485 of length 19 | 19.83 |
| 90 | 1373314410 | 501554760 | 0.36521 | 51 | 122775516 of length 20 | 20.00 |
Using this rather inefficient GP script, you can find right-truncatable primes in arbitrary bases:
rtp(base)={
local(pd=vector(eulerphi(base)),pdl=length(pd),fl=0,bl=[],sp=0,j,k);
j=0;for(i=1,base-1,if(gcd(i,base)==1,j++;pd[j]=i));
forprime(p=2,base-1,fl++;bl=concat(bl,[p]));
while(length(bl)>0,
nb=[];
for(i=1,length(bl),
p=bl[i]*base;
k=0;
for(j=1,pdl,if(ispseudoprime(p+pd[j]),k++;nb=concat(nb,[p+pd[j]])));
fl+=k;sp+=!k
);
bl=nb
);
[fl,sp]
}
It finds them in increasing order of number of digits, which makes it very inefficient memory wise.
Another hastily constructed page by Phil Carmody
Home /
Maths /
index.html